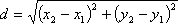1. The Process of Optimization: The purpose is to find a maximum or minimum of a specific equation when given a set of equations with at least two variables.. Start by solving for a variable in one equation. Plug that variable into another equation and find the equation's derivative. Set this derivative equal to zero and solve for the other variable.
2. Example: Find the point on the line y= 2x+3 that is closest to the origin (0,0).
1) For this problem, the distance formula will need to be used because we are trying to find the "closest" point. The answer will be a minimum.
2) Because we have the point (0,0), we will first plug that into our distance formula. Turning the x1 and y1 into zeros.
3) The next step is to plug in our Y value which is 2x+3.
4) The next step would be to square both sides to eliminate the square root. It would then look like this: d^2= x^2 + (2x+3)^2
5) Then we distribute the square to the 2x+3 giving us d^2= x^2+4x^2+12x+9
6) We then use the power rule to find the derivative of the new equation. 2d= 2x +8x +12.
7) We set the derivative equal to zero and solve. 0= 10x+12
8) X= -6/5
9) Now that we know the value of x, we plug it back in to the original equation to solve of Y. y=2(-6/5)+3
10) y=3/5
11) The point that is on the line y= 2x+3 and is closest to the origin is (-6/5, 3/5).
3. Find two equations for the derivative: f'(x)= 6x^2-10x-1
1) f(x)= 2x^3-5x^2-x
2) f(x)= 2x^3-5x^2-x +5