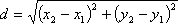The Final Calculus Blog Post

1. Identify why these topics are tough.

• Using U-substitution to evaluate integrals is difficult to set up. It is sometimes hard to know which value will be the U and which value will be the DU.
• Finding the area between two curves is challenging when I forget to find which function is on top and when there are more than two places where the functions intersect.
• Finding the volume of a region using cylindrical shells is difficult because I often confuse this method with the washer method.
• Finding the volume of a region using the washer method is difficult because I often confuse this method with cylindrical shells.
• Using the limit definition to find the area under the curve also proves to be difficult because I do not remember the limit definition. 

2. Do the Problems

• U-SUB
• Find the definite integral of x(1 - 3x2)4dx u=1-3x^2, du=-6xdx, -1/30(1-3x^2)^5 +c
• Find the definite integral of  (1+sec(x))2(sec(x)tan(x))dx u= 1 + sec, du= sec(piX)tan(piX)dx, ((2-3x)^3)/3 +c
• Find f(x) when f(x) = x((2-3x)^1/2)dx u= 2-3x, du=-3dx, (2/45(2-3x)^5/2)(-4/27(2-3x)^3/2)+c
• Cylindrical Shells
• Find the volume of the region bounded by y = 2x3, y=2x, x = 1, and x = 2;
• revolved about the y- axis 2pi from 0 to 1 x(2x^3-2x)dx, 232/15pi
• Washer Method
• Find volume of area bounded by x = 0, y = x +4 and y = 12x2 revolved around x = -1 pi from -1 to 0, (x+4)^2 -(1/2x^2)^2dx, 737/60pi
• Limit Definition
• Evaluate the following using the limit definition and using integrationf(x) = 4x - 5 on  [1, 5] The Summation of 4/n 4(1+4i/n) -5, The answer is 28.
• Area Between the Curves
• Find area of the region bounded by : f(x) = 2x-2    g(x) = -x2-2x+3 Interval -5 to 1, (-x^2-2x+3) - (2x-2), 108/3
• Find area of the region bounded by : f(x) = 2x3-1, g(x) = 2x-1 Interval 0 to 1, (2x-1)-(2x^3-1) The answer for this half is one half. We must multiply by to because the function is cubic and symmetrical across the y-axis. The answer is just one.

3. Create a problem that is similar.

• U-Sub
• Y= sec^2(x)tan^3(x), U= tan(x), Du= sec^2(x)dx, 1/4tan^4(x)+c
• Cylindrical Shells
• y=x-x^2, y=0, about x=2, 2pi integral of 0 to 1, (2-x)(x-x^2)dx, pi/2
• Washer Method
• y=x, y=x^2 about the x-axis. pi integral of 0 to 1, ((y^1/2)^2)-(y)^2dy, pi/6
• Limit Definition
• 2x^2-1 on [1, 5] limit as n approaches infinity of the summation of 4/n 2(1 + 4i/n)^2 -1, 236/3
• Area Between the Curves
• y= x^2-2x-4, y=x Integral -1 to 4, (x) - (x^2-2x-4)dx, 125/6

Blog Post #9

1.) Identify the difference between rotating around a vertical line and a horizontal line. When rotated around a vertical line, the washers are stacked vertically, one on top of another. When rotated around a horizontal line, the washers are stacked horizontally, side by side. Which variable goes with each one? When rotated around a vertical line, you will be working in terms of y. When rotated around a horizontal line, you will be working in terms of x.

2.) What is the difference between creating a washer and a disk? When a washer is created, there is a hole within the figure, resulting in subtraction. When a disc is created, there is no subtraction. A washer is created when the shaded region of the figure does not connect with the line that the function is being rotated around. A disc is created when the shaded region of the line does connect with the line that the function is being rotated around.

3.) Identify two examples that use rotating about a vertical and horizontal line.

Example 1: Rotated about a horizontal line.

X=0, Y=X^2, Y=4, Rotated around Y=6

Because it is being rotated around a horizontal line, it is in terms of X. We can use X=0 and Y= 4 to determine our interval. When we plug 4 in for Y in Y=X^2, we get X=2. We already know that X=0, so we know the interval is from 0 to 2. We know that x^2 is our radius because it is what changes. We are required to subtract our radius from six because we need to exclude the portions between 0 and 2 that are not filled in. We also need to subtract 6 from 4 because there is a a gap on that interval. We will also pull out pi.  It will look like pi(0 to 2) ((6-x^2)^2)-(6-4)^2. When you simplify it will be pi(36-12x^2+x^4-4 dx). When you take the anti derivative, you get pi(32x-4x^3+1/5x^5). When you plug in the interval 2 (You do not need to plug in zero as it would be subtracted from 2 and zero will give you zero) you should get pi192/5.

Example 2: Rotated about a vertical line.
X=0, X=y-y^2, revolved around the y-axis.
To find our interval, we must set y-y^2 equal to zero. When we do, we get 0=y(1-y) which factors to give us y=0 and y=1. Our interval is 0 to 1. Because it revolves around a vertical line, it will be in terms of y. Our radius will be y-y^2 because it is what changes. The setup will be pi(0 to 1) ((y-y^2)^2)dy. The anti derivative is pi(0 to 1) y^3-1/2y^4+1/5y^5. All we have to do is plug in one because the simplification of zero will be subtracted from the simplification of one. When one is plugged in it should be pi/30.  

Blog Post #8

Identify Three Learning Targets

Learning Target Number 1: I can approximate the area under a curve using left and right endpoints.
     a.) You must first decide the width of the rectangles or the change in X of the function. This is a preference as to how accurate you wish to be when finding the area under the curve. The smaller the width or change in x, the more accurate the calculation will be as there are more rectangles.
     b.) The next step is to set up a summation to accurately represent the rectangles being used to calculate the area under the curve. The summation should include n= the number of rectangles, delta x= the width of the rectangles and which endpoint you will start with. (The summation with number of rectangles "n" above and i=1 below of delta x times the function of the lower limit plus i times delta x.) Or the summation of Delta X= (lower limit + I delta X)
     Ex. 4-2x^2 on [0,12] In this case, because I am not a fan of being accurate and I am lazy, I will have six triangles and my triangle widths will be two. Starting from the left endpoint, I will include zero and exclude twelve. Starting from the right endpoint, I will include twelve and exclude zero. From the left endpoint it will be 2 (f(0)+f(2)+f(4)+f(6)+f(8)+f(10))=-832
From the right endpoint it will be 2(f(2)+f(4)+f(6)+f(8)+f(10)+f(12))=-1408
What usually "trips me up the most" is knowing how accurate to be with my calculation. (Knowing how many rectangles to use for my area.)

Learning Target Number 2: I can find the area under the curve using the Riemman's Summation.
     a.) During Riemman's Summation, there is an infinite amount of rectangles. This is very similar to the previous learning target except that we use n as the number of rectangles, we take the problem as n approaches infinity, and delta x is the interval distance over n.
The limit as n approaches infinity of the summation of delta x times f(lower limit + i Delta x)
     b.) The rest of the process is exactly the same except there will be more reducing of summations. It is also essential to understand that the summation of i^2 is (2n^3 + 3n^2 + n)/6.
Ex. 4-2x^2 on [0,12]
1.) Take the limit as n approaches infinity of the summation of 12/n -2(0+12i/n)^2 + 4 2.) Distribute the square and then the negative two. 3.) Put the 12/n in front of the summation. 4.) Separate the i^2 from i^2/n^2 5.) Distribute the summation. 6.) Distribute the 12/n. 7.) Cancel the denominator of the summation of i^2. 8.) Disregard remaining terms containing "n" and simplify. 9.) The answer should be -1104.
The most difficult part for me when using Riemman's Summation is remembering the summations of i and i^2.

Learning Target Number 3: I can find the area under a curve using the fundamental theorem of calculus.
     a.) Find the anti derivative of the original function. Plug your upper value into the anti derivative and plug the lower value into the anti derivative. subtract the higher from the lower.
Ex. 4-2x^2 on [0,12]
4x-2/3x^3 + c is the anti derivative.
4(12)-2/3(12)^3 +c -  (4(0)-2/3(0)^3+c = -1104 -0 = -1104
The most difficult part when using the fundamental theorem of calculus part two is remembering which interval is first.

Blog Post #7

1. The Process of Optimization: The purpose is to find a maximum or minimum of a specific equation when given a set of equations with at least two variables.. Start by solving for a variable in one equation. Plug that variable into another equation and find the equation's derivative. Set this derivative equal to zero and solve for the other variable. 

2. Example: Find the point on the line y= 2x+3 that is closest to the origin (0,0).

     1) For this problem, the distance formula will need to be used because we are trying to find the "closest" point. The answer will be a minimum. 

     2) Because we have the point (0,0), we will first plug that into our distance formula. Turning the x1 and y1 into zeros.

     3) The next step is to plug in our Y value which is 2x+3. 

     4) The next step would be to square both sides to eliminate the square root. It would then look like this: d^2= x^2 + (2x+3)^2

     5) Then we distribute the square to the 2x+3 giving us d^2= x^2+4x^2+12x+9

     6) We then use the power rule to find the derivative of the new equation. 2d= 2x +8x +12.

     7) We set the derivative equal to zero and solve. 0= 10x+12

     8) X= -6/5

     9) Now that we know the value of x, we plug it back in to the original equation to solve of Y. y=2(-6/5)+3

     10) y=3/5

     11) The point that is on the line y= 2x+3 and is closest to the origin is (-6/5, 3/5).

3. Find two equations for the derivative: f'(x)= 6x^2-10x-1

      1) f(x)= 2x^3-5x^2-x

      2) f(x)= 2x^3-5x^2-x +5